３次ベジェ曲線アニメ

３次ベジェ曲線の原理

それでは、３次ベジェ曲線上の各点の座標 [X(t),Y(t)] の計算方法を考えていきます。
それには、３次ベジェ曲線の原理について理解する必要があります。
まずは基礎的事項を理解します。
中学生でもわかるベジェ曲線
を参照してください。

３次ベジェ関数式

ベジェ関数式は、

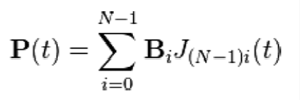
で記述されます。
ウィキペディアベジェ曲線
を参照してください。

Bi は制御（ハンドル）点です。
t は 0～1 できざみ 0.02 とすると 50 ポイント位置指定します。
N = 2 の時

２点を直線で結びます。
i = 0,1 で終わりです。
N = 3 の時

始点と終点の間に制御点（片ハンドル）１個を含む曲線です。
i = 0,1,2 で終わりです。
あまり自由度はありません。
N = 4（３次ベジェ曲線）の時

始点と終点の間に制御点（片ハンドル）２個を含む曲線です。
i = 0,1,2,3 で終わりです。

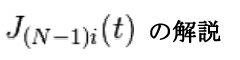
これはブレディング関数で n = N－1 とすると

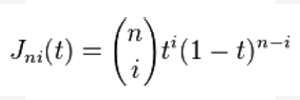
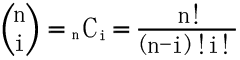
となります。
二項定理階乗
については、各リンクを参照してください。
0 ! = 1
1 ! = 1
2 ! = 2
3 ! = 6

N=4（３次ベジェ曲線）の解析

i = 0 ,1,2,3 について解析していきます。
n = N－1 = 3

一旦整理

P(t)
= B0・J30(t) + B1・J31(t) + B2・J32(t) + B3・J33(t)
= B0 (1－t)3 + B1・3t (1－t)2 + B2・3t2(1－t) + B3・t3

Bi の解析

始点　　B0 (X0,Y0)
制御点 B1 (X1,Y1)
制御点 B2 (X2,Y2)
終点　　B3 (X3,Y3)
とすると
X(t) = X0 (1－t)3 + X1・3t (1－t)2 + X2・3t2(1－t) + X3・t3
Y(t) = Y0 (1－t)3 + Y1・3t (1－t)2 + Y2・3t2(1－t) + Y3・t3
となり、これが３次ベジェ関数となります。
即ち、t を０～１まで刻みを 0.02 程度にして、％を t×100 にすれば、３次ベジェ曲線関数 function を記述できます。

イラストレータによるシミュレーション

それでは、この３次ベジェ関数で書いた図形が具体的にどうなるのかイラストレータで確認します。
使用する Illustrator ファイルは
３次ベジェ曲線運動 Ai ファイルダウンロ－ド
から入手することができます。
圧縮されていますので、解凍してから使用してください。

ダウンロ－ドファイルを参照

ダウンロ－ドした 3_bezier0.zip を解凍し、AI ファイル 3_bezier0.ai を開きます。
心配な方はあらかじめウィルスチェックをしましょう。
これを見ながらここからの説明を読んでください。
アンカ

B0 、B3 、２個のアンカを打ちます。
B0 が始点、B3 が終点となります。
ハンドル

始点、終点にそれぞれハンドルを設定します。
ハンドル先端が、B1 ～ B2 となります。
B0 始点、B3 終点にはそれぞれ片ハンドルを設定します。
まとめ

イラストレ－タで描写しハンドル先端位置を決めれば、それと同じ曲線を関数化し移動軌跡を作成することができます。

３次ベジェ曲線アニメファイル作成に進む
３次ベジェ曲線アニメ作成概要に戻る